Finite Impulse Response (FIR) Interpolator
- RISCV_DSP_ATTRIBUTE void riscv_fir_interpolate_f32 (const riscv_fir_interpolate_instance_f32 *S, const float32_t *pSrc, float32_t *pDst, uint32_t blockSize)
- RISCV_DSP_ATTRIBUTE riscv_status riscv_fir_interpolate_init_f32 (riscv_fir_interpolate_instance_f32 *S, uint8_t L, uint16_t numTaps, const float32_t *pCoeffs, float32_t *pState, uint32_t blockSize)
- RISCV_DSP_ATTRIBUTE riscv_status riscv_fir_interpolate_init_q15 (riscv_fir_interpolate_instance_q15 *S, uint8_t L, uint16_t numTaps, const q15_t *pCoeffs, q15_t *pState, uint32_t blockSize)
- RISCV_DSP_ATTRIBUTE riscv_status riscv_fir_interpolate_init_q31 (riscv_fir_interpolate_instance_q31 *S, uint8_t L, uint16_t numTaps, const q31_t *pCoeffs, q31_t *pState, uint32_t blockSize)
- RISCV_DSP_ATTRIBUTE void riscv_fir_interpolate_q15 (const riscv_fir_interpolate_instance_q15 *S, const q15_t *pSrc, q15_t *pDst, uint32_t blockSize)
- RISCV_DSP_ATTRIBUTE void riscv_fir_interpolate_q31 (const riscv_fir_interpolate_instance_q31 *S, const q31_t *pSrc, q31_t *pDst, uint32_t blockSize)
- group Finite Impulse Response (FIR) Interpolator
These functions combine an upsampler (zero stuffer) and an FIR filter. They are used in multirate systems for increasing the sample rate of a signal without introducing high frequency images. Conceptually, the functions are equivalent to the block diagram below:
After upsampling by a factor of
L, the signal should be filtered by a lowpass filter with a normalized cutoff frequency of1/Lin order to eliminate high frequency copies of the spectrum. The user of the function is responsible for providing the filter coefficients.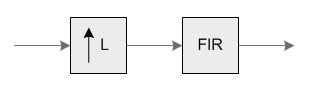
The FIR interpolator functions provided in the NMSIS DSP Library combine the upsampler and FIR filter in an efficient manner. The upsampler inserts
L-1zeros between each sample. Instead of multiplying by these zero values, the FIR filter is designed to skip them. This leads to an efficient implementation without any wasted effort. The functions operate on blocks of input and output data.pSrcpoints to an array ofblockSizeinput values andpDstpoints to an array ofblockSize*Loutput values.The library provides separate functions for Q15, Q31, and floating-point data types.
- Algorithm
The functions use a polyphase filter structure: This approach is more efficient than straightforward upsample-then-filter algorithms. With this method the computation is reduced by a factor of
1/Lwhen compared to using a standard FIR filter.pCoeffspoints to a coefficient array of sizenumTaps.numTapsmust be a multiple of the interpolation factorLand this is checked by the initialization functions. Internally, the function divides the FIR filter’s impulse response into shorter filters of lengthphaseLength=numTaps/L. Coefficients are stored in time reversed order.pStatepoints to a state array of sizeblockSize + phaseLength - 1. Samples in the state buffer are stored in the order:The state variables are updated after each block of data is processed, the coefficients are untouched.
- Instance Structure
The coefficients and state variables for a filter are stored together in an instance data structure. A separate instance structure must be defined for each filter. Coefficient arrays may be shared among several instances while state variable array should be allocated separately. There are separate instance structure declarations for each of the 3 supported data types.
- Initialization Functions
There is also an associated initialization function for each data type. The initialization function performs the following operations:
Sets the values of the internal structure fields.
Zeros out the values in the state buffer.
Checks to make sure that the length of the filter is a multiple of the interpolation factor. To do this manually without calling the init function, assign the follow subfields of the instance structure: L (interpolation factor), pCoeffs, phaseLength (numTaps / L), pState. Also set all of the values in pState to zero.
Use of the initialization function is optional. However, if the initialization function is used, then the instance structure cannot be placed into a const data section. To place an instance structure into a const data section, the instance structure must be manually initialized. The code below statically initializes each of the 3 different data type filter instance structures
where
Lis the interpolation factor;phaseLength=numTaps/Lis the length of each of the shorter FIR filters used internally,pCoeffsis the address of the coefficient buffer;pStateis the address of the state buffer. Be sure to set the values in the state buffer to zeros when doing static initialization.- Fixed-Point Behavior
Care must be taken when using the fixed-point versions of the FIR interpolate filter functions. In particular, the overflow and saturation behavior of the accumulator used in each function must be considered. Refer to the function specific documentation below for usage guidelines.
Functions
- RISCV_DSP_ATTRIBUTE void riscv_fir_interpolate_f32 (const riscv_fir_interpolate_instance_f32 *S, const float32_t *pSrc, float32_t *pDst, uint32_t blockSize)
Processing function for floating-point FIR interpolator.
Processing function for the floating-point FIR interpolator.
- Parameters:
S – [in] points to an instance of the floating-point FIR interpolator structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of input samples to process
- RISCV_DSP_ATTRIBUTE riscv_status riscv_fir_interpolate_init_f32 (riscv_fir_interpolate_instance_f32 *S, uint8_t L, uint16_t numTaps, const float32_t *pCoeffs, float32_t *pState, uint32_t blockSize)
Initialization function for the floating-point FIR interpolator.
- Details
pCoeffspoints to the array of filter coefficients stored in time reversed order:The length of the filter
numTapsmust be a multiple of the interpolation factorL.pStatepoints to the array of state variables.pStateis of length(numTaps/L)+blockSize-1words whereblockSizeis the number of input samples processed by each call toriscv_fir_interpolate_f32().
- Parameters:
S – [inout] points to an instance of the floating-point FIR interpolator structure
L – [in] upsample factor
numTaps – [in] number of filter coefficients in the filter
pCoeffs – [in] points to the filter coefficient buffer
pState – [in] points to the state buffer
blockSize – [in] number of input samples to process per call
- Returns:
execution status
RISCV_MATH_SUCCESS : Operation successful
RISCV_MATH_ARGUMENT_ERROR : filter length
numTapsis not a multiple of the interpolation factorL
- RISCV_DSP_ATTRIBUTE riscv_status riscv_fir_interpolate_init_q15 (riscv_fir_interpolate_instance_q15 *S, uint8_t L, uint16_t numTaps, const q15_t *pCoeffs, q15_t *pState, uint32_t blockSize)
Initialization function for the Q15 FIR interpolator.
- Details
pCoeffspoints to the array of filter coefficients stored in time reversed order: The length of the filternumTapsmust be a multiple of the interpolation factorL.pStatepoints to the array of state variables.pStateis of length(numTaps/L)+blockSize-1words whereblockSizeis the number of input samples processed by each call toriscv_fir_interpolate_q15().
- Parameters:
S – [inout] points to an instance of the Q15 FIR interpolator structure
L – [in] upsample factor
numTaps – [in] number of filter coefficients in the filter
pCoeffs – [in] points to the filter coefficient buffer
pState – [in] points to the state buffer
blockSize – [in] number of input samples to process per call
- Returns:
execution status
RISCV_MATH_SUCCESS : Operation successful
RISCV_MATH_ARGUMENT_ERROR : filter length
numTapsis not a multiple of the interpolation factorL
- RISCV_DSP_ATTRIBUTE riscv_status riscv_fir_interpolate_init_q31 (riscv_fir_interpolate_instance_q31 *S, uint8_t L, uint16_t numTaps, const q31_t *pCoeffs, q31_t *pState, uint32_t blockSize)
Initialization function for the Q31 FIR interpolator.
- Details
pCoeffspoints to the array of filter coefficients stored in time reversed order: The length of the filternumTapsmust be a multiple of the interpolation factorL.pStatepoints to the array of state variables.pStateis of length(numTaps/L)+blockSize-1words whereblockSizeis the number of input samples processed by each call toriscv_fir_interpolate_q31().
- Parameters:
S – [inout] points to an instance of the Q31 FIR interpolator structure
L – [in] upsample factor
numTaps – [in] number of filter coefficients in the filter
pCoeffs – [in] points to the filter coefficient buffer
pState – [in] points to the state buffer
blockSize – [in] number of input samples to process per call
- Returns:
execution status
RISCV_MATH_SUCCESS : Operation successful
RISCV_MATH_ARGUMENT_ERROR : filter length
numTapsis not a multiple of the interpolation factorL
- RISCV_DSP_ATTRIBUTE void riscv_fir_interpolate_q15 (const riscv_fir_interpolate_instance_q15 *S, const q15_t *pSrc, q15_t *pDst, uint32_t blockSize)
Processing function for the Q15 FIR interpolator.
- Scaling and Overflow Behavior
The function is implemented using a 64-bit internal accumulator. Both coefficients and state variables are represented in 1.15 format and multiplications yield a 2.30 result. The 2.30 intermediate results are accumulated in a 64-bit accumulator in 34.30 format. There is no risk of internal overflow with this approach and the full precision of intermediate multiplications is preserved. After all additions have been performed, the accumulator is truncated to 34.15 format by discarding low 15 bits. Lastly, the accumulator is saturated to yield a result in 1.15 format.
- Parameters:
S – [in] points to an instance of the Q15 FIR interpolator structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of input samples to process
- RISCV_DSP_ATTRIBUTE void riscv_fir_interpolate_q31 (const riscv_fir_interpolate_instance_q31 *S, const q31_t *pSrc, q31_t *pDst, uint32_t blockSize)
Processing function for the Q31 FIR interpolator.
- Scaling and Overflow Behavior
The function is implemented using an internal 64-bit accumulator. The accumulator has a 2.62 format and maintains full precision of the intermediate multiplication results but provides only a single guard bit. Thus, if the accumulator result overflows it wraps around rather than clip. In order to avoid overflows completely the input signal must be scaled down by
1/(numTaps/L). sincenumTaps/Ladditions occur per output sample. After all multiply-accumulates are performed, the 2.62 accumulator is truncated to 1.32 format and then saturated to 1.31 format.
- Parameters:
S – [in] points to an instance of the Q31 FIR interpolator structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of input samples to process