Finite Impulse Response (FIR) Filters

void riscv_fir_f16(const riscv_fir_instance_f16 *S, const float16_t *pSrc, float16_t *pDst, uint32_t blockSize)

void riscv_fir_f32(const riscv_fir_instance_f32 *S, const float32_t *pSrc, float32_t *pDst, uint32_t blockSize)

void riscv_fir_f64(const riscv_fir_instance_f64 *S, const float64_t *pSrc, float64_t *pDst, uint32_t blockSize)

void riscv_fir_fast_q15(const riscv_fir_instance_q15 *S, const q15_t *pSrc, q15_t *pDst, uint32_t blockSize)

void riscv_fir_fast_q31(const riscv_fir_instance_q31 *S, const q31_t *pSrc, q31_t *pDst, uint32_t blockSize)

void riscv_fir_init_f16(riscv_fir_instance_f16 *S, uint16_t numTaps, const float16_t *pCoeffs, float16_t *pState, uint32_t blockSize)

void riscv_fir_init_f32(riscv_fir_instance_f32 *S, uint16_t numTaps, const float32_t *pCoeffs, float32_t *pState, uint32_t blockSize)

void riscv_fir_init_f64(riscv_fir_instance_f64 *S, uint16_t numTaps, const float64_t *pCoeffs, float64_t *pState, uint32_t blockSize)

riscv_status riscv_fir_init_q15(riscv_fir_instance_q15 *S, uint16_t numTaps, const q15_t *pCoeffs, q15_t *pState, uint32_t blockSize)

void riscv_fir_init_q31(riscv_fir_instance_q31 *S, uint16_t numTaps, const q31_t *pCoeffs, q31_t *pState, uint32_t blockSize)

void riscv_fir_init_q7(riscv_fir_instance_q7 *S, uint16_t numTaps, const q7_t *pCoeffs, q7_t *pState, uint32_t blockSize)

void riscv_fir_q15(const riscv_fir_instance_q15 *S, const q15_t *pSrc, q15_t *pDst, uint32_t blockSize)

void riscv_fir_q31(const riscv_fir_instance_q31 *S, const q31_t *pSrc, q31_t *pDst, uint32_t blockSize)

void riscv_fir_q7(const riscv_fir_instance_q7 *S, const q7_t *pSrc, q7_t *pDst, uint32_t blockSize)

group FIR

This set of functions implements Finite Impulse Response (FIR) filters for Q7, Q15, Q31, and floating-point data types. Fast versions of Q15 and Q31 are also provided. The functions operate on blocks of input and output data and each call to the function processes blockSize samples through the filter. pSrc and pDst points to input and output arrays containing blockSize values.

The array length L must be a multiple of x. L = x * a :

x is 4 for f32
x is 4 for q31
x is 4 for f16 (so managed like the f32 version and not like the q15 one)
x is 8 for q15
x is 16 for q7

Algorithm

The FIR filter algorithm is based upon a sequence of multiply-accumulate (MAC) operations. Each filter coefficient b[n] is multiplied by a state variable which equals a previous input sample x[n].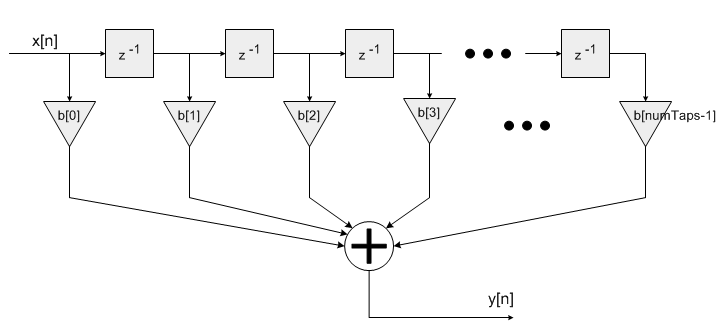

../../../_images/FIR.png

pCoeffs points to a coefficient array of size numTaps. Coefficients are stored in time reversed order.

pState points to a state array of size numTaps + blockSize - 1. Samples in the state buffer are stored in the following order.

Note that the length of the state buffer exceeds the length of the coefficient array by blockSize-1. The increased state buffer length allows circular addressing, which is traditionally used in the FIR filters, to be avoided and yields a significant speed improvement. The state variables are updated after each block of data is processed; the coefficients are untouched.

Instance Structure

The coefficients and state variables for a filter are stored together in an instance data structure. A separate instance structure must be defined for each filter. Coefficient arrays may be shared among several instances while state variable arrays cannot be shared. There are separate instance structure declarations for each of the 4 supported data types.

Initialization Functions

There is also an associated initialization function for each data type. The initialization function performs the following operations:

Sets the values of the internal structure fields.
Zeros out the values in the state buffer. To do this manually without calling the init function, assign the follow subfields of the instance structure: numTaps, pCoeffs, pState. Also set all of the values in pState to zero.

Use of the initialization function is optional. However, if the initialization function is used, then the instance structure cannot be placed into a const data section. To place an instance structure into a const data section, the instance structure must be manually initialized. Set the values in the state buffer to zeros before static initialization. The code below statically initializes each of the 4 different data type filter instance structures where numTaps is the number of filter coefficients in the filter; pState is the address of the state buffer; pCoeffs is the address of the coefficient buffer.

Initialization of Helium version

For Helium version the array of coefficients must be padded with zero to contain a full number of lanes.

The additional coefficients (x * a - numTaps) must be set to 0. numTaps is still set to its right value in the init function. It means that the implementation may require to read more coefficients due to the vectorization and to avoid having to manage too many different cases in the code.

Helium state buffer

The state buffer must contain some additional temporary data used during the computation but which is not the state of the FIR. The first A samples are temporary data. The remaining samples are the state of the FIR filter.

So the state buffer has size numTaps + A + blockSize - 1 :

A is blockSize for f32
A is 8*ceil(blockSize/8) for f16
A is 8*ceil(blockSize/4) for q31
A is 0 for other datatypes (q15 and q7)

Fixed-Point Behavior

Care must be taken when using the fixed-point versions of the FIR filter functions. In particular, the overflow and saturation behavior of the accumulator used in each function must be considered. Refer to the function specific documentation below for usage guidelines.

Functions

void riscv_fir_f16(const riscv_fir_instance_f16 *S, const float16_t *pSrc, float16_t *pDst, uint32_t blockSize)

Processing function for floating-point FIR filter.

Processing function for the floating-point FIR filter.

Parameters

S – [in] points to an instance of the floating-point FIR filter structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of samples to process

Returns

none

void riscv_fir_f32(const riscv_fir_instance_f32 *S, const float32_t *pSrc, float32_t *pDst, uint32_t blockSize)

Processing function for floating-point FIR filter.

Processing function for the floating-point FIR filter.

Parameters

S – [in] points to an instance of the floating-point FIR filter structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of samples to process

Returns

none

void riscv_fir_f64(const riscv_fir_instance_f64 *S, const float64_t *pSrc, float64_t *pDst, uint32_t blockSize)

Processing function for floating-point FIR filter.

Processing function for the floating-point FIR filter.

Parameters

S – [in] points to an instance of the floating-point FIR filter structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of samples to process

Returns

none

void riscv_fir_fast_q15(const riscv_fir_instance_q15 *S, const q15_t *pSrc, q15_t *pDst, uint32_t blockSize)

Processing function for the Q15 FIR filter (fast version).

Processing function for the fast Q15 FIR filter (fast version).

Remark

Refer to riscv_fir_q15() for a slower implementation of this function which uses 64-bit accumulation to avoid wrap around distortion. Both the slow and the fast versions use the same instance structure. Use function riscv_fir_init_q15() to initialize the filter structure.

Scaling and Overflow Behavior: This fast version uses a 32-bit accumulator with 2.30 format. The accumulator maintains full precision of the intermediate multiplication results but provides only a single guard bit. Thus, if the accumulator result overflows it wraps around and distorts the result. In order to avoid overflows completely the input signal must be scaled down by log2(numTaps) bits. The 2.30 accumulator is then truncated to 2.15 format and saturated to yield the 1.15 result.

Parameters

S – [in] points to an instance of the Q15 FIR filter structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of samples to process

Returns

none

void riscv_fir_fast_q31(const riscv_fir_instance_q31 *S, const q31_t *pSrc, q31_t *pDst, uint32_t blockSize)

Processing function for the Q31 FIR filter (fast version).

Processing function for the fast Q31 FIR filter (fast version).

Remark

Refer to riscv_fir_q31() for a slower implementation of this function which uses a 64-bit accumulator to provide higher precision. Both the slow and the fast versions use the same instance structure. Use function riscv_fir_init_q31() to initialize the filter structure.

Scaling and Overflow Behavior: This function is optimized for speed at the expense of fixed-point precision and overflow protection. The result of each 1.31 x 1.31 multiplication is truncated to 2.30 format. These intermediate results are added to a 2.30 accumulator. Finally, the accumulator is saturated and converted to a 1.31 result. The fast version has the same overflow behavior as the standard version and provides less precision since it discards the low 32 bits of each multiplication result. In order to avoid overflows completely the input signal must be scaled down by log2(numTaps) bits.

Parameters

S – [in] points to an instance of the Q31 structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of samples to process

Returns

none

void riscv_fir_init_f16(riscv_fir_instance_f16 *S, uint16_t numTaps, const float16_t *pCoeffs, float16_t *pState, uint32_t blockSize)

Initialization function for the floating-point FIR filter.

Details: pCoeffs points to the array of filter coefficients stored in time reversed order:
: pState points to the array of state variables. pState is of length numTaps+blockSize-1 samples (except for Helium - see below), where blockSize is the number of input samples processed by each call to riscv_fir_f16().
Initialization of Helium version: For Helium version the array of coefficients must be a multiple of 4 (4a) even if less then 4a coefficients are defined in the FIR. The additional coefficients (4a - numTaps) must be set to 0. numTaps is still set to its right value in the init function. It means that the implementation may require to read more coefficients due to the vectorization and to avoid having to manage too many different cases in the code.
Helium state buffer: The state buffer must contain some additional temporary data used during the computation but which is not the state of the FIR. The first 8*ceil(blockSize/8) samples are temporary data. The remaining samples are the state of the FIR filter. So the state buffer has size numTaps + 8*ceil(blockSize/8) + blockSize - 1

Parameters

S – [inout] points to an instance of the floating-point FIR filter structure
numTaps – [in] number of filter coefficients in the filter
pCoeffs – [in] points to the filter coefficients buffer
pState – [in] points to the state buffer
blockSize – [in] number of samples processed per call

Returns

none

void riscv_fir_init_f32(riscv_fir_instance_f32 *S, uint16_t numTaps, const float32_t *pCoeffs, float32_t *pState, uint32_t blockSize)

Initialization function for the floating-point FIR filter.

Details: pCoeffs points to the array of filter coefficients stored in time reversed order:
: pState points to the array of state variables and some working memory for the Helium version. pState is of length numTaps+blockSize-1 samples (except for Helium - see below), where blockSize is the number of input samples processed by each call to riscv_fir_f32().
Initialization of Helium version: For Helium version the array of coefficients must be a multiple of 4 (4a) even if less then 4a coefficients are defined in the FIR. The additional coefficients (4a - numTaps) must be set to 0. numTaps is still set to its right value in the init function. It means that the implementation may require to read more coefficients due to the vectorization and to avoid having to manage too many different cases in the code.
Helium state buffer: The state buffer must contain some additional temporary data used during the computation but which is not the state of the FIR. The first blockSize samples are temporary data. The remaining samples are the state of the FIR filter. So the state buffer has size numTaps + 2 * blockSize - 1

Parameters

S – [inout] points to an instance of the floating-point FIR filter structure
numTaps – [in] number of filter coefficients in the filter
pCoeffs – [in] points to the filter coefficients buffer
pState – [in] points to the state buffer
blockSize – [in] number of samples processed per call

Returns

none

void riscv_fir_init_f64(riscv_fir_instance_f64 *S, uint16_t numTaps, const float64_t *pCoeffs, float64_t *pState, uint32_t blockSize)

Initialization function for the floating-point FIR filter.

Details: pCoeffs points to the array of filter coefficients stored in time reversed order:
: pState points to the array of state variables. pState is of length numTaps+blockSize-1 samples, where blockSize is the number of input samples processed by each call to riscv_fir_f64().
: There is no Helium version of the fir F64.

Parameters

S – [inout] points to an instance of the floating-point FIR filter structure
numTaps – [in] number of filter coefficients in the filter
pCoeffs – [in] points to the filter coefficients buffer
pState – [in] points to the state buffer
blockSize – [in] number of samples processed per call

Returns

none

riscv_status riscv_fir_init_q15(riscv_fir_instance_q15 *S, uint16_t numTaps, const q15_t *pCoeffs, q15_t *pState, uint32_t blockSize)

Initialization function for the Q15 FIR filter.

Details: pCoeffs points to the array of filter coefficients stored in time reversed order: Note that numTaps must be even and greater than or equal to 4. To implement an odd length filter simply increase numTaps by 1 and set the last coefficient to zero. For example, to implement a filter with numTaps=3 and coefficients set numTaps=4 and use the coefficients: Similarly, to implement a two point filter set numTaps=4 and use the coefficients: pState points to the array of state variables. pState is of length numTaps+blockSize, when running on RISC-V Core with DSP enabled and is of length numTaps+blockSize-1, when running on RISC-V Core without DSP where blockSize is the number of input samples processed by each call to riscv_fir_q15().
Initialization of Helium version: For Helium version the array of coefficients must be a multiple of 8 (8a) even if less then 8a coefficients are defined in the FIR. The additional coefficients (8a - numTaps) must be set to 0. numTaps is still set to its right value in the init function. It means that the implementation may require to read more coefficients due to the vectorization and to avoid having to manage too many different cases in the code.

Parameters

S – [inout] points to an instance of the Q15 FIR filter structure.
numTaps – [in] number of filter coefficients in the filter. Must be even and greater than or equal to 4.
pCoeffs – [in] points to the filter coefficients buffer.
pState – [in] points to the state buffer.
blockSize – [in] number of samples processed per call.

Returns

execution status

RISCV_MATH_SUCCESS : Operation successful
RISCV_MATH_ARGUMENT_ERROR : numTaps is not greater than or equal to 4 and even

void riscv_fir_init_q31(riscv_fir_instance_q31 *S, uint16_t numTaps, const q31_t *pCoeffs, q31_t *pState, uint32_t blockSize)

Initialization function for the Q31 FIR filter.

Details: pCoeffs points to the array of filter coefficients stored in time reversed order: pState points to the array of state variables. pState is of length numTaps+blockSize-1 samples (except for Helium - see below), where blockSize is the number of input samples processed by each call to riscv_fir_q31().
Initialization of Helium version: For Helium version the array of coefficients must be a multiple of 4 (4a) even if less then 4a coefficients are defined in the FIR. The additional coefficients (4a - numTaps) must be set to 0. numTaps is still set to its right value in the init function. It means that the implementation may require to read more coefficients due to the vectorization and to avoid having to manage too many different cases in the code.
Helium state buffer: The state buffer must contain some additional temporary data used during the computation but which is not the state of the FIR. The first 2*4*ceil(blockSize/4) samples are temporary data. The remaining samples are the state of the FIR filter. So the state buffer has size numTaps + 8*ceil(blockSize/4) + blockSize - 1

Parameters

S – [inout] points to an instance of the Q31 FIR filter structure
numTaps – [in] number of filter coefficients in the filter
pCoeffs – [in] points to the filter coefficients buffer
pState – [in] points to the state buffer
blockSize – [in] number of samples processed

Returns

none

void riscv_fir_init_q7(riscv_fir_instance_q7 *S, uint16_t numTaps, const q7_t *pCoeffs, q7_t *pState, uint32_t blockSize)

Initialization function for the Q7 FIR filter.

Details: pCoeffs points to the array of filter coefficients stored in time reversed order:
: pState points to the array of state variables. pState is of length numTaps+blockSize-1 samples, where blockSize is the number of input samples processed by each call to riscv_fir_q7().
Initialization of Helium version: For Helium version the array of coefficients must be a multiple of 16 (16a) even if less then 16a coefficients are defined in the FIR. The additional coefficients (16a - numTaps) must be set to 0. numTaps is still set to its right value in the init function. It means that the implementation may require to read more coefficients due to the vectorization and to avoid having to manage too many different cases in the code.

Parameters

S – [inout] points to an instance of the Q7 FIR filter structure
numTaps – [in] number of filter coefficients in the filter
pCoeffs – [in] points to the filter coefficients buffer
pState – [in] points to the state buffer
blockSize – [in] number of samples processed

Returns

none

void riscv_fir_q15(const riscv_fir_instance_q15 *S, const q15_t *pSrc, q15_t *pDst, uint32_t blockSize)

Processing function for the Q15 FIR filter.

Remark

Refer to riscv_fir_fast_q15() for a faster but less precise implementation of this function.

Scaling and Overflow Behavior: The function is implemented using a 64-bit internal accumulator. Both coefficients and state variables are represented in 1.15 format and multiplications yield a 2.30 result. The 2.30 intermediate results are accumulated in a 64-bit accumulator in 34.30 format. There is no risk of internal overflow with this approach and the full precision of intermediate multiplications is preserved. After all additions have been performed, the accumulator is truncated to 34.15 format by discarding low 15 bits. Lastly, the accumulator is saturated to yield a result in 1.15 format.

Parameters

S – [in] points to an instance of the Q15 FIR filter structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of samples to process

Returns

none

void riscv_fir_q31(const riscv_fir_instance_q31 *S, const q31_t *pSrc, q31_t *pDst, uint32_t blockSize)

Processing function for Q31 FIR filter.

Processing function for the Q31 FIR filter.

Remark

Refer to riscv_fir_fast_q31() for a faster but less precise implementation of this filter.

Scaling and Overflow Behavior: The function is implemented using an internal 64-bit accumulator. The accumulator has a 2.62 format and maintains full precision of the intermediate multiplication results but provides only a single guard bit. Thus, if the accumulator result overflows it wraps around rather than clip. In order to avoid overflows completely the input signal must be scaled down by log2(numTaps) bits. After all multiply-accumulates are performed, the 2.62 accumulator is right shifted by 31 bits and saturated to 1.31 format to yield the final result.

Parameters

S – [in] points to an instance of the Q31 FIR filter structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of samples to process

Returns

none

void riscv_fir_q7(const riscv_fir_instance_q7 *S, const q7_t *pSrc, q7_t *pDst, uint32_t blockSize)

Processing function for Q7 FIR filter.

Processing function for the Q7 FIR filter.

Scaling and Overflow Behavior: The function is implemented using a 32-bit internal accumulator. Both coefficients and state variables are represented in 1.7 format and multiplications yield a 2.14 result. The 2.14 intermediate results are accumulated in a 32-bit accumulator in 18.14 format. There is no risk of internal overflow with this approach and the full precision of intermediate multiplications is preserved. The accumulator is converted to 18.7 format by discarding the low 7 bits. Finally, the result is truncated to 1.7 format.

Parameters

S – [in] points to an instance of the Q7 FIR filter structure
pSrc – [in] points to the block of input data
pDst – [out] points to the block of output data
blockSize – [in] number of samples to process

Returns

none